Мы привыкли к трехмерному пространству и уже начинаем привыкать к четырехмерному пространству-времени.

О многомерности пространства говорят много, но осязать ее как трехмерное пространство мы не умеем. Подчеркну – именно не умеем, а не не можем.

Как же нам увидеть, например, четвертую пространственную координату. Не временную, а именно пространственную координату. У многих может возникнуть вопрос: а существует ли эта координата в природе физически, так как координаты X и Y в виде тропинок на земле, или координата Z в виде лесенки?

Во-первых, все эти три координаты не зависимы друг от друга. Объект может двигаться сколько угодно, и с любой скоростью по одной из этих осей, не изменяя ничего на других осях, как будь то, они не существуют.

Во-вторых, чтобы определить положение объекта в этом пространстве следует указать значения трех координат.

Спрашивается: существует ли такая четвертая координата в виде какого-нибудь физического явления, удовлетворяющая этим двум требованиям?   То есть, мы могли бы двигаться по этой координате, не изменяя параметров других координат, и если мы не зададим значение этой четвертой координаты, то мы не узнаем местоположение объекта. Вот мы и поищем такую координату

Представим пастуха пасущего стадо из четырех коров.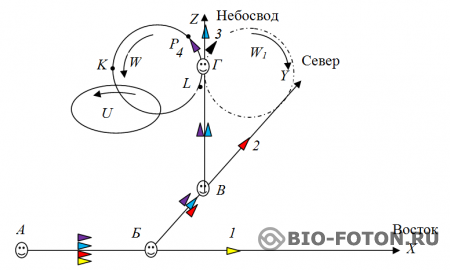

Пастух, начиная с точки А, гонит четыре коровы по оси X на восток. Он видит их всех. И вдруг в точке Б он обнаруживает, что три коровы исчезли. На оси X он видит всего одну корову 1. Кустарник и деревья мешают пастуху видеть что-нибудь вне оси X.

Он доходит до точки Б и обнаруживает, что три коровы повернули на север по оси Y. Они увидели пробел в кустах, и пошли по нему, а корова 1 пошла прямо. Пастух побрел за тремя коровами.

 В точке В он опять видит пропажу двух коров.  Он остановился в точке В и начал осматривать окрестности. Посмотрел на запад, на восток и даже оглянулся назад на юг, может быть, прошел мимо них. Но нигде ничего не было. Только корова номер 2 лениво плелась на север. В этот момент он обратил внимание на высокую скалу, выступавшую на тропинку, протоптанную коровами. Он поднял свои глаза вверх и обнаружил, что его две коровы, как альпинисты, карабкаются вверх по скале. Наверное, пастуха звали Декарт. А во времена Декарта коровы умели лазить по скалам.

Что же делать? Пришлось и пастуху двинуться за этими двумя коровами. Хозяевам коров номер один и два он позвонил и сказал, в каком направлении идут их коровы, чтобы они их по тем направлениям и встречают.

Но в точке Г новая беда – исчезла еще одна корова. Корова 3 лезет вверх, пусть ее хозяин снимает вертолетом или еще как-нибудь, если она сама не сползет со скалы. Но где же корова номер 4?

Наш пастух вертел головой по всем направлениям: и не север, и на юг, и на восток, и на запад, и  вверх, и вниз. Нигде коровы нет. Правда, когда смотрел на запад что-то быстро про мигнуло в точке К, вроде коровы, но потом ничего не было. Наверное, померещилось. Пастух поднялся еще выше точки Г и там осмотрелся по всем направлениям, но все равно ничего не увидел. “Надо обратиться за помощью” – подумал он.

Был у него друг Шредингер, он его и позвал на помощь. Тот пришел, встал на точку Г и начал осматривать направления. И ему тоже показалось, что что-то появилось в точке P. Затем он мельком увидел это в точке L, Kи других точках. И еще Шредингер заметил, что если объект похожий на корову появляется в районе точек LиP, то он дольше виден, нежели в случае появления его в районе точки K. Он сразу же сообразил, что корова вероятнее всего находится в районе точек LилиP. Он написал формулу, по которой нужно искать корову: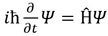

Вот уже почти сто лет пастух так и ищет корову. Промелькнет корова, он к ней направится, а ее там уже нет.

Почему так получается? А очень просто – потому что свет распространяется прямолинейно, и пастух, не вращаясь, не может корову держать в поле своего зрения. Вот если бы свет распространялся, например, по окружности, то пастух на координате W корову видел бы все время, а на прямых координатах видел бы корову мельком.

Об этой координате было известно уже давно. Как пишет в своей книге “Элегантная Вселенная” Брайан Грин:

“…в 1919 г. малоизвестный польский математик Теодор Калуца из Кёнигсбергского университета дерзнул бросить вызов очевидному — он предположил, что в действительности Вселенная может иметь не три измерения, число измерений может бытьбольше”.

Теперь к трем пространственным координатам добавились, по мнению Калуцы и Клейна, четвертые маленькие, свернутые, координаты, которые распространены по всему пространству. Пространство приобрело примерно такой вид:

Какие недостатки в данном предположении Калуцы-Клейна?

Первое. Создается впечатление, как будь то, эти свернутые координаты представлены каким-то субстратом и торчат в пространстве. Но ведь этого в природе не существует. Координаты это просто траектории, по которым движется или на которых находится какой-то материальный объект. Это касается всех координат, в том числе и прямоугольных.

Второе. Грин пишет:

“… измерения, которые туго скручены в ничтожно малой области — столь малой, что она не может быть обнаружена даже с помощью самого современного экспериментального оборудования”.

Спрашивается, что скручено – материал вакуума или материал эфира, то есть, то из чего состоит пространство? То из чего состоит пространство скручено туго в ничтожно малой области. Что получаются сгустки пространства? И что – эти колечки или спирали фиксированных размеров или располагаются в определенном диапазоне пространства по величине? Вот, например, корова может ходить по кругу различной величины. Или тот большой круг координаты W не есть координата? Маленький круг координата, а большой круг не координата.

“Клейн объединил первоначальное предположение Калуцы с некоторыми идеями бурно развивавшейся квантовой механики. Его расчёты показали, что дополнительное циклическое измерение по размерам сопоставимо с планковской длиной, что выходит далеко за рамки современных возможностей экспериментального изучения”.

Как видите, движение коровы по кругу не есть дополнительное циклическое движение. Ну, хорошо, корова есть корова, с нее спрос мал, не хочет она бегать по кругу.

А как трактовать путь Магеллана? Он отправился в путь из родной гавани и плыл все время в одном направлении и через некоторое время оказался снова в родной гавани. Двигаясь по прямоугольной координате такой эффект не получить. Можно ли считать этот путь циклическим измерением? Ведь он мог снова повторить этот путь. Или этот цикл слишком большой и его нельзя считать циклическим? Хорошо.

Тогда путь электрона в атоме то же не есть дополнительное циклическое измерение? Даже если мы и не знаем точного места нахождения электрона в атоме, то все равно должны признать, что он совершает там какие-то циклические движения. Пусть даже будут это вероятностные зоны нахождения электрона, но они циклические. Может быть не круговые, а эллиптические или еще какие-нибудь замкнутые кривые. И размеры эти кривых очень далеки от планковской длины.

Что еще может двигаться по этой координате? Протоны, кварки, глюоны? Что? Гравитон? Так в последнем случае тела падали бы по кривой. Фотон не умеет двигаться криво (не указывайте на коэффициент преломления), он летит прямо. Может быть, струны движутся по этим координатам? Так нет же. Они наматываются на координаты.

Что не думай, а фиолетовая корова номер 4 пошла по четвертой пространственной координате W.

А если бы в стаде была черная корова, то она могла бы вообще пойти по координате W₁ являющейся зеркальной координате W.

В случае обнаружения вкусной травки вне координаты W, фиолетовая корова могла оставить движение по этой координате и двинуться по координате U. А это уже пятое измерение и, причем, оно может быть циклическим.

К сожалению Калуца не пошел дальше четвертого измерения. Хотя “Калуца объединил теорию гравитации Эйнштейна с максвелловской  теорией электромагнитного поля”, его теорию не восприняли всерьез и забыли о ней на 60 лет.

Но потом появились теории, которые требовали большего количества измерений. Появились объемные координаты в виде шара, тора и другие. Но все эти дополнительные измерения все равно считаются маленькими и свернуты в понятную нам форму.

Так выглядит пространство с 4 и 5 дополнительным измерением. Вам это ничего не напоминает? Верно, это обычные широта и долгота, которыми человечество пользуется много лет. Если бы кто видел нашу Землю движущуюся в трехмерном пространстве, то наше движение по мередианам или параллелям представлялось бы такому наблюдателю как движение по свернутым дополнительным координатам. Движение в глубь шара или от шара представлялось бы как 6-е дополнительное измерение.

В природе все эти измерения заполнены до предела. Электрон в проводнике или электроннолучевой трубке, если нет отклоняющих полей, электрического или магнитного, движется в трехмерном измерении. Но если электрон находится в составе атома, а атом движется в трехмерном пространстве, то электрон в дополнение к этому движется еще и в атоме условно по мередианам и параллелям. Да еще и переходит с уровня на уровень, то есть по радиусу атома. Электрон в атоме живет в шестимерном пространстве.

К сожалению  этого никто не замечает. После того как Шредингер написал свою волновую функцию и заменил координаты электрона в атоме вероятностью никто уже около ста лет и не пытается понять движение электрона в атоме, не пытается понять какие силы работают в атоме. Что там можно изучать в атоме с несколькими десятками электронов, если они представлены вероятностями, то есть каждый электрон может находится в атоме в любом месте с той или иной вероятностью? О каких координатах может вестись речь – о прямоугольных, косоугольных, свернутых или развернутых?  Можно ли в этом случае вести речь о синтезе атомов или даже о химических реакциях? А об устройстве электрона никто и не заикается. А ведь он вращается или, возможно, по его поверхности распространяется электромагнитная волна фотона. И чтобы знать местоположение элементов фотона надо использовать следующие дополнительные измерения.