Изменение размеров физических тел.

Данное понятие в специальную теорию относительности ввел Альберт Эйнштейн и, к сожалению, ввел с ошибкой.

В § 2. “Об относительности длин и промежутков времени” своей статьи “К электродинамике движущихся тел” А. Эйнштейн пишет:

“а) наблюдатель движется вместе с указанным масштабом и с измеряемым стержнем и измеряет длину стержня непосредственно путем прикладывания масштаба так же, как если бы измеряемый стержень, наблюдатель и масштаб находились в покое;

б) наблюдатель устанавливает с помощью расставленных в покоящейся системе синхронных, в смысле § 1, покоящихся часов, в каких точках покоящейся системы находятся начало и конец измеряемого стержня в определенный момент времени t. Расстояние между этими двумя точками, измеренное использованным выше, но уже покоящимся масштабом, есть длина, которую можно обозначить как «длину стержня».

Согласно принципу относительности, длина, определяемая операцией «а», которую мы будем называть «длиной стержня в движущейся системе», должна равняться длине l покоящегося стержня.

Длину, устанавливаемую операцией «б», которую мы будем называть «длиной (движущегося) стержня в покоящейся системе», мы определим, основываясь на наших двух принципах, и найдем, что она отлична от l”.

Действительно дальнейшие рассуждения показывают, что длина стержня в движущейся системе оказывается меньше чем в неподвижной системе. В § 4 приводится пример с движущимся шаром. В неподвижной системе тело имевшее форму шара, в движущейся системе превращается в эллипсоид, причем полуоси, ориентированные по координатам y и z, остались прежними равными радиусу шара R. В тоже время ось по направлению движения изменилась и стала равной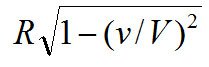

Чем больше скорость, тем больше будет сжиматься эллипсоид, вплоть до превращения его в плоскую фигуру. Так мыслил Эйнштейн, если перевод его статьи точен. Частично с этим согласиться можно, но не со всем.

Представим, что у нас имеется некий третейский судья в виде наблюдателя, и он наблюдает за двумя находящимися рядом шарами. Пока шары находятся рядом и покоятся, они не теряют своей формы. Потом на один из шаров начала воздействовать некоторая сила. Шар начал ускоряться, изменяя свою скорость. Кроме того шар, согласно теории относительности, начал сплющиваться, превращаясь в эллипсоид. Такую же картину должен видеть наблюдатель из неподвижного шара. В это же время наблюдатель в неподвижном шаре должен обозревать данное тело в виде шара.         

Так сжались ли объективно стержень и шар при увеличении их скорости? И если сжались то как? Действительно ли сжались они в плоскую фигуру? Какие физические силы их сжали? Как изменилась внутренняя структура твердого тела? И изменилась ли? Вот на эти вопросы мы и попытаемся сейчас ответить. Первое, что приходит в голову это, примерно, такой процесс сжатия.  Рассмотрим процесс сжатия стержня (Рис. 14.).

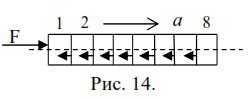
Разобьем мысленно стержень части. При приложении силы F к стержню, последний получит некоторое ускорение а. Согласно третьему закону Ньютона каждая часть стержня будет сопротивляться приложенной силе, сжимая все части, расположенные между ней и приложенной силой. Больше всего будет сжата часть 1 и менее всего будет сжата часть 8. Но что будет со стержнем после снятия воздействующей на него силы? Если сила не превысила предел упругости, стержень примет начальные свои размеры, хотя скорость он приобрел другую. А потом, когда мы сжимали стержень вдоль, он увеличивал свои другие размеры, становился толще.  Особенно это заметно на мяче. Сжатие мяча по одной координате приводит к возрастанию его размеров по другим координатам. Плохая модель. 

А что же происходит с параметрами электрона в действительности? Мы знаем, что при ускорении электрон излучает фотоны. В результате этого он переходит на другой уровень. Опыт и здравый смысл подсказывают, что при этом он изменяет свое расстояние от ядра атома (см. статью “Устройство атома”). После того как электрон потерял часть своей электромагнитной энергии, он с этим потерял часть заряда. Чтобы электрон с меньшим зарядом удерживался ядром, он должен приблизиться к ядру. Естественно, приближение электрона к ядру приводит к уменьшению размеров атома и, в конечном счете, приводит к уменьшению всего тела. Так как в размерах уменьшаются все электроны, движущегося тела, то тело уменьшается не в одном каком-то одном направлении, а во всем объеме. Может быть, существуют некоторые анизотропные материалы, которые изменяют свои размеры не одинаково во всех направлениях, но это происходит из-за особой структуры вещества.   

Существуют ли примеры, подтверждающие нашу модель изменения размеров тел при изменении их скорости? Не смотря на кажущуюся удаленность теории относительности от повседневной жизни, примеров проявления изменения объемов тел при изменении их скоростных режимов можно наблюдать много.

Первое это наблюдаемое нами повсеместное сокращение тел при их охлаждении. В самом деле, всем известно, что при нагревании все тела расширяются. Ну, а при охлаждении, естественно, сжимаются, причем по всем направлениям. А почему мы думаем, что при охлаждении скорость электронов увеличивается? Всю жизнь учим, что при понижении температуры тепловое движение всех частиц уменьшается и, в пределе, при абсолютной температуре  -273К, движение прекращается вообще, а тут, вдруг, говорится о возрастании скорости. Да, действительно, атомы и молекулы при понижении температуры толкаются между собой все меньше и меньше, но скорость электрона в атоме становится все больше и больше. Электрон, если можно так выразиться, все больше и больше “прижимается” к ядру. В результате тело сжимается. Можно еще чем-нибудь подтвердить эту мысль? Да. Давайте пойдем обратным путем. Будем повышать температуру тела, тело расширяется, электрон удаляется от ядра, его связь с ядром уменьшается и наступает момент, когда фотон определенной энергии может этот электрон выбить из атома (фотоэффект) и электрон практически останавливается. То есть электрон поглотил фотон и замедлил свою скорость. Казалось бы, электрон приобрел дополнительную энергию и должен был бы двигаться энергичнее, но нет, его масса, то есть внутренняя энергия возросла, а кинетическая энергия  , возможно, осталась прежней. Это значит, что электрон снизил свою скорость. Дальнейшее повышение температуры приводит к поглощению тепловых фотонов электронами следующих уровней, они теряют связь с ядром, и так вплоть до образования плазмы.

Вторым примером изменения объема тел является явление, подмеченное Бернулли. Чем больше скорость течения вещества в трубе, тем меньшее давление создает вещество. Если по трубе с переменным сечением прогонять, например, воду и манометрами измерять давление в разных сечениях трубы, то там где труба тоньше там и меньшее давление. Если Вы спросите маститого профессора, почему так, то он ответит что там, где тоньше труба там большая скорость тока воды и поэтому меньшее давление. Вот и весь ответ. А почему при большей скорости меньшее давление Вам он не скажет. А ответ прост. Давление создается толкающимися молекулами. При увеличении скорости молекулы, точнее их электроны, излучают фотоны, теряя часть заряда и массы, из-за этого они становятся меньше. Среда разрежается и создает меньшее давление.

Третье это подъемная сила. Движение молекул воздуха сверху крыла самолета более быстрое, нежели под низом крыла из-за специальной его конструкции. В результате этого давление сверху крыла меньшее, чем снизу. Эта разница и составляет подъемную силу. Практически получается, более разреженный воздух тянет крылья вверх.

Четвертый пример – сопло Лаваля. Это сопло имеет чуть расширяющийся выход для газов. Оказывается, что если в двигателе сопло заканчивается самой узкой частью своего течения, то тяга двигателя такая-то. Если же в конце узкого сечения добавить нечто в виде расширяющегося раструба, то тяга двигателя увеличивается. Это и подметил Лаваль. За счет чего же увеличивается тяга? Это можно объяснить только с квантовых позиций. При выходе из сопла молекулы теряют свою скорость, как молекулы воды в трубе при переходе с узкого сечения в более широкое сечение. Они начинают поглощать фотоны и увеличиваться в объеме. Если сопло открытое,  (Рис. 15), то получается какая-то тяга F_Т. В сопле Лаваля, расширяющиеся частицы ударяются об наклонную стенку сопла с силой расширения Fр, которую можно разложить на две силы: Fл – силу Лаваля и F – силу, разрывающую сопло. Вторая сила никакого отношения к тяге двигателя не имеет, а сила Лаваля добавляется к тяге.

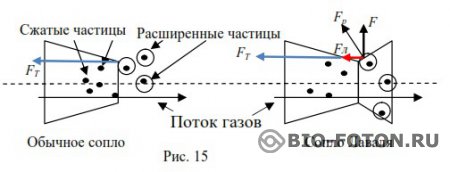
Не следует думать, что поскольку относительная скорость истекающих газов и сопла довольно большая (до 4 км/сек), то расширяющаяся частица будет оказывать незначительную силу Fр на сопло. Скорость поглощения фотонов идет на несколько порядков быстрее, нежели скорость движения сопла.

Пятый пример это инверсный след после самолета или движущегося велосипедиста. Ускоренные частицы воздуха от движения некого тела убывают в объеме, создавая определенный вакуум. Истекающие газы реактивного самолета заставляют молекулы воздуха излучить более мощные фотоны, которые на нашей Земле более редки (см. статью “О чем нам может поведать абсолютно черное тело?”). Зона инверсного следа оказалась на склоне горба кривой излучения абсолютно черного тела и теперь необходимо время, чтобы частицы инверсного следа поглотили соответствующие фотоны и стали такими же частицами, которые их окружают. Согласно изложенной модели изменения размеров тела по одной  из оси их распространения при увеличении или уменьшения их абсолютной скорости конфигурация тел не изменяется, а уменьшаются или увеличиваются все размеры одновременно. Возможно, что коэффициентом пропорциональности изменения размеров является релятивистский коэффициент.

Справедливой оказывается формула: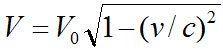

где V – объем тела в движущейся системе, V₀ – объем тела в неподвижной системе координат, а v – скорость ИСО.