Теория струн. Часть 11
Брайан Грин описал не “Элегантную Вселенную”, а нарисовал какой-то ребус.
В предыдущей главе мы пытались понять минимальный размер измерений.
Но не столько удалось это понять, как пришлось принять это на веру, без надежды уразуметь необходимость этого.
На минимум ограничения мы наложили. А на максимум? Что R может быть сколь угодно большим? Вот R садового шланга, мне кажется, значительно больше планковского размера. И это циклическое измерение. А если замкнуть концы садового шланга, то нелепо отрицать, что это циклическое измерение. Для муравья это Вселенная. И если ему будет достаточно пищи на этом шланге, то он будет жить, не подозревая, по каким измерения он ползает. Никакие ограничения в этом случае на размер измерений невозможно наложить.
Но теория струн предполагает, что циклические измерения очень маленькие, а с другой стороны R может быть любым. Ну и как можно свернуть толщину или длину шланга до планковских размеров или даже микро размеров? Может быть, математические выкладки показывают, что это возможно, но душа этого не принимает и приходится просто верить. Неприятие некоторых таких положений существует и в иных других теориях.
Зеркальная симметрия
В общей теории относительности, как и в «традиционной» геометрии, окружность радиуса R отличается от окружности радиуса 1/R, что кажется незыблемым и очевидным, а в теории струн эти окружности физически неразличимы.
Теоретикам такое положение понравилось, и они задались вопросом:
не существует ли геометрических структур пространства, отличающихся друг от друга ещё сильнее (не только размером, но, возможно, и видом), но, тем не менее, физически неразличимых в теории струн?
По счастливой случайности оказалось, что такие неразличимые физически, но отличающиеся геометрически структуры пространства существуют. Дело в том, что геометрия структуры отвечает за появление семейств частиц. Три отверстия в пространстве отвечают за три семейства. Таблица 1.1. Но отверстия могут быть разными. Одни отверстия могут проходить через все 6 измерений, например, в многообразии Колаби-Яу, другие через 6 или 2 измерения. Я вырезал из 6-ти мерного пространства 3 измерения.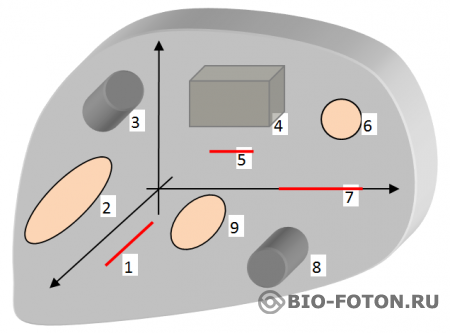
Отверстия 3, 4, 8 трехмерные. Они на границе данного пространства выходят в виде некоторых площадей. Отверстия 2, 6, 9 двухмерные и на границе пространства они имеют вид линий. Отверстия 1, 5, 7 одномерные и на границе видны в виде точек. Эти отверстия лучше представлять в виде отверстий проделанных червем в яблоке. Трехмерный червяк проделает трехмерную дыру. Плоский червяк проделает двухмерную дыру, а одномерный червь проделает одномерное отверстие.
Так вот ученые Ленс Диксон, Вольфганган Лерхе, Вафа и Николас Уорнер предположили, или, может быть, это у них родилось на кончике пера, что за качество и количество семейств отвечает только количество отверстий, а не их размерность. То есть пространство с отверстиями 1, 2 и 3 родит ровно такое же семейство, как и пространство с отверстиями 3, 4 и 6 или отверстиями 1, 9 и 7. Как видите, за одно и то же отвечает довольно много пространств, что должно облегчать их поиск.
Так и решился выше поставленный вопрос. Но появились новые свойства пространств Колаби-Яу.
Оказывается, что пространства Колаби-Яу существуют не сами по себе как объективная реальность, а это образования, которые мы можем изменять и конструировать по своему усмотрению. Как пишет Брайан:
Плессер и я заинтересовались методами построения путём математических преобразований новых доселе неизвестных многообразий Калаби–Яу из заданного многообразия Калаби–Яу.
Очень продуктивным методом построения новых многообразий явился метод орбифолдов, который заключается в склеивании определенных точек исходного многообразия. Но точки должны выбираться так, чтобы новое многообразие тоже было многообразием Колаби-Яу. Интересное дело, а что же получится, если мы склеим не те точки? Если склеились не те точки, то это и не новое, но уже и не старое многообразие. А что? Конечно это глупые вопросы. Не понимаешь математических выкладок, так и не спрашивай. Нам вообще не понятно из чего это пространство состоит. Думаем что из точек, а из каких …
Важно то, что после правильного склеивания получаются такие многообразия: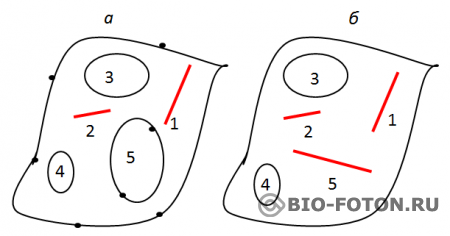
Число отверстий нечётной размерности нового многообразия будет равно числу отверстий чётнойразмерности исходного, и наоборот. Это, в частности, означает, что полное число отверстий, а, следовательно, и число семейств частиц в двух многообразиях будут одинаковыми, хотя из-за чётно-нечётных замен вид многообразий и их фундаментальные геометрические свойства будут существенно разными.
После склеивания некоторых точек в пространстве аполучилось пространство б, в котором одно двухмерное отверстие 5 исчезло, и появилось третье одномерное отверстие 5. Возможно, изменились и размеры всех или части отверстий. В многообразии а три двухмерных отверстия и два одномерных отверстия. А многообразие бсодержит три одномерных отверстия и два двухмерных отверстия. Общее количество отверстий одинаково в этих многообразиях.
Многообразия а и б называются зеркальными многообразиями, они различны в геометрическом смысле, но тождественны в физическом смысле.
Дальше оказалось, что у каждого многообразия есть такая зеркальная пара и что все физические свойства зеркальных пар одинаковы.
Таким образом, Брайан оказался причастен к открытию зеркальной симметрии в теории струн.
Что нам дает зеркальная симметрия?
Физика и математика зеркальной симметрии
Интересно, что физическое описывает зеркальная симметрия? Обещание обнадеживающее:
Зеркальная симметрия, в частности, даёт мощное средство для исследования как физических аспектов теории струн, так и математических аспектов теории пространств Калаби–Яу.
Если вы прочтете данный раздел книги до конца, то увидите, что физический аспект теории струн заключается в том чтобы:
- вычислить физические характеристики — массы и заряды, — соответствующие выбору одного из возможных пространств Калаби–Яу в качестве дополнительных измерений.
- задача заключалась в вычислении числа сфер, которые можно упаковать внутрь некоторого пространства Калаби–Яу.
Во втором случае все оказалось просто. При расчетах с помощью зеркальной симметрии внутри этого пространства оказалось 317 206 375 сфер. В то же время физики, занимаясь обычными расчетами, обнаружили в этом же пространстве 2 682 549 425 сферы. Видите, какая разница. Они долго спорили кто прав, но потом физики обнаружили ошибку в своих расчетах и зеркальная симметрия победила. Вот как теория струн помогла физикам. Может быть, вас смущает такое количество сфер и вы скажете, что можно бы взять сферы побольше или поменьше и не мучится над расчетами. Нет у математиков так нельзя, то есть так не корректно. Возможно, это какие-то одиночные сферы, или такие сферы которые должны заполнять пространство полностью без пробелов и наложений, или выполнится еще какое-нибудь математическое условие. Это все неважно. Главное люди были при деле.
А с первым случаем возникают не понятности. Выбираю я одно из возможных пространств Колаби-Яу. А какие пространства возможны, а какие не возможны? Если они есть, то, наверное, они и возможны. Что у Брайана прячется за словом возможных? Может быть, у возможныхтри отверстия? Или у возможных на измерениях намотаны струны? Или в этих пространствах плавают не намотанные струны? По какому признаку их выбирать? Для нас ведь важна струна, ибо она олицетворяет частицу, хотя и подправляется пространством. Ясно, что пространства с тремя отверстиями для нас не интересны: все массы и заряды по ним уже рассчитаны. Так что в принципе можно брать любое другое пространство, рассчитывать по нему другие семейства частиц других Вселенных. Может быть, это пригодится в будущем, когда мы откроем другую Вселенную с предсказанными и вычисленными при помощи зеркальной симметрии частицы с данными зарядами и массами. В данном случае теория струн освещает путь физикам.
А как дело обстоит в реальности? Существует ли зеркальная симметрия? Если да, то, как она связана с нашим миром? Ответы на эти вопросы положительны и понятны.
Зеркальная симметрия в природе называется хиральность. В зеркале вы видите свое симметричное изображение. Руки, ноги, уши, а, соответственно, перчатки, ботинки все это хирально, то есть зеркально симметрично. Но нас должно интересовать не это, а хиральность молекул и в частности сахара – дезоксирибозы. Не будь этой хиральности сахара, не было бы и нас, при условии, что заменителя нет.
Дезоксирибоза при строительстве дезоксирибонуклеиновой кислоты участвует как правый сахар. При соединении такого сахара с азотистым основанием он излучает или поглощает фотоны правой поляризации. Левую поляризацию такой сахар не видит. Это происходит при репликации ДНК.
Но для построения организма по плану, заложенному в ДНК, мы должны с нее снимать информацию. Информация с ДНК снимается в виде генов, определенных участков ДНК. Гены это небольшие участки молекулы. На этих участках строятся молекулы РНК, а потом на этих РНК строятся белки. Я здесь не буду рассказывать, как это происходит, это описано в соответствующих статьях. Только скажу, что для построения РНК требуется, чтобы все сахара, относящиеся к транскрибируемому, то есть из которого снимается информация, гену, поменяли свою ориентацию с правой на левую. В определенном атоме сахара электрон, участвующий в выборе хиральности, изменяет ориентацию спина и начинает излучать и поглощать левые фотоны. Получается левый сахар зеркальный исходному правому. Весь ген становится зеркальный исходному. И на ветви ДНК, без ее расплетения, строится РНК. Так РНК в левом состоянии доходит до аминокислот, у которых левая ориентация.
Вот так зеркальная симметрия участвует в жизни природы. Если до этого дойдет теория струн, то ей честь и хвала. А что она нам приготовила, дальше посмотрим.





