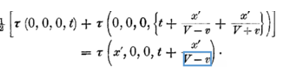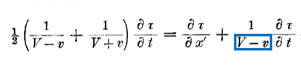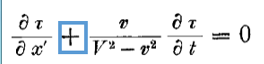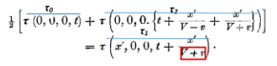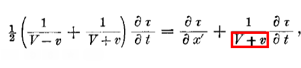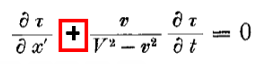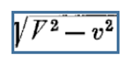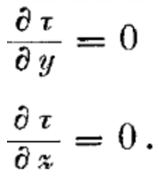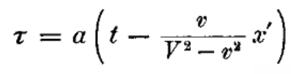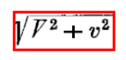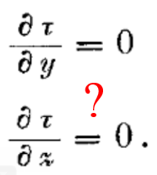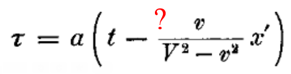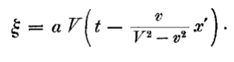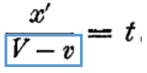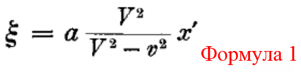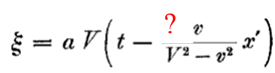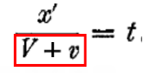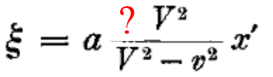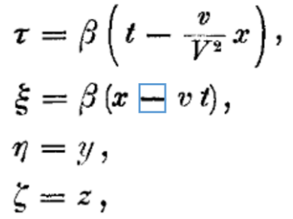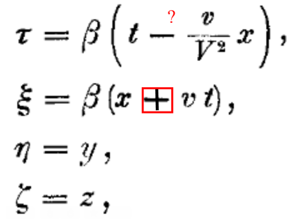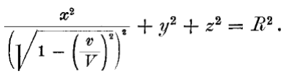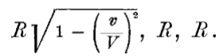Изменение размеров тел. Теория относительности.
В статье “К электродинамике движущихся тел” Эйнштейн рассказывает об изменение размеров тел при их движении. Я хочу попросить о помощи кого-нибудь из математиков разобраться в данной работе Эйнштейна.
И то не во всей работе, а только в ее части. А именно понять, как получился данный релятивистский коэффициент. Я думаю, что для математика это простая задача.
Дело в том, что Эйнштейн для теории преобразования координат и времени рассматривал удаляющиеся системы и у него начальные данные для уравнений получились такие: скорость света по осям Z и Y в движущейся системе, видимая неподвижным наблюдателем, была равна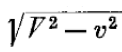 
, а по оси X – равна V-v. Но в силу однородности пространства, о чем, пишет сам Эйнштейн, по крайней мере в этой же работе, с телом должно происходить одно и то же, не зависимо от того, в каком направлении оно движется. И вот возникает вопрос, что будет видеть неподвижный наблюдатель, если он будет видеть одновременно два тела, движущиеся навстречу друг другу. Одно тело, допустим стержень, будет приближаться к наблюдателю, а другой стержень удаляться. На практике, глядя вдоль рельсов, на два встречных поезда, мы видим, что удаляющийся поезд уменьшается в объеме, а не только в длине, а встречный, напротив, увеличивается в объеме. Конечно это аналогия, но возможно то же произойдет в теории относительности. Я выписываю два почти одинаковых текста: один текст Эйнштейна (слева) с его начальными данными и справа текст, который должен быть при допущении сближения двух систем. Где мог я в силу своих способностей скорректировал текст Эйнштейна к новым исходным данным, но не везде. Не хватает знаний. Ну, например, откуда появилась неизвестная функция а, да еще и зависящая от скорости? Я возможно что-то не так скорректировал. Там, где я что-то не понимаю, я вставляю свой текст.
Если решение задачи будет такое, как получил Эйнштейн, то это укрепит его позицию и его будут меньше ругать. Если же такое решение невозможно осуществить или оно даст другие результаты, то специальную теорию относительности надо как-то модифицировать. Но это уже будет не голословное обвинение Эйнштейна в не точности СТО, а математически доказанное, чему многие поклоняются.
|
§ 3. Теория преобразования координат и времени от покоящейся системы к системе, равномерно прямолинейно движущейся относительно первой
Пусть в «покоящемся» пространстве даны две координатные системы, каждая с тремя взаимно- перпендикулярными осями, выходящими из одной точки. Пусть оси X обеих систем совпадают, а оси Y и Z соответственно параллельны. Пусть каждая система снабжена масштабом и некоторым числом часов, и пусть оба масштаба и все часы в обеих системах в точности одинаковы. Пусть теперь началу координат одной из этих систем (k) сообщается (постоянная) скорость v в направлении убывающих значений x другой, покоящейся системы (K) эта скорость передается также координатным осям, а также соответствующим масштабам и часам. |
§ 3. Теория преобразования координат и времени от покоящейся системы к системе, равномерно прямолинейно движущейся относительно первой
Пусть в «покоящемся» пространстве даны две координатные системы, каждая с тремя взаимно- перпендикулярными осями, выходящими из одной точки. Пусть оси X обеих систем совпадают, а оси Y и Z соответственно параллельны. Пусть каждая система снабжена масштабом и некоторым числом часов, и пусть оба масштаба и все часы в обеих системах в точности одинаковы. Пусть теперь началу координат одной из этих систем (k) сообщается (постоянная) скорость v в направлении возрастающих значений x другой, покоящейся системы (K) эта скорость передается также координатным осям, а также соответствующим масштабам и часам. |
Мы имеем право сообщать скорость в любом направлении. Поезда могут ездить не только из Москвы в Тверь, но и наоборот: из Твери в Москву.
|
Тогда каждому моменту времени t покоящейся системы (K) соответствует определенное положение осей движущейся системы, и мы из соображений симметрия вправе допустить, что движение системы k может быть таким, что оси движущейся системы в момент времени t (через t всегда будет обозначаться время покоящейся системы) будут параллельны осям покоящейся системы. Представим себе теперь, что пространство размечено как в покоящейся системе K посредством покоящегося в ней масштаба, так и в движущейся системе k посредством движущегося с ней масштаба, и что, таким образом, получены координаты x, y, z и соответственно ξ, η, ζ. Пусть посредством покоящихся часов, находящихся в покоящейся системе, и с помощью световых сигналов указанным в §1 способом определяется время t покоящейся системы для всех тех точек последней, в которых находятся часы. Пусть далее таким же образом определяется время τ движущейся системы для всех точек этой системы, в которых находятся покоящиеся относительно последней часы, указанным в §1 способом световых сигналов между точками, в которых эти часы находятся. Каждому набору значений x, y, z, t, которые полностью определяют место и время событий в покоящейся системе, соответствует набор значений ξ, η, ζ, τ, устанавливающий это событие в системе k, и теперь необходимо найти систему уравнений, связывающих эти величины. Прежде всего ясно, что эти уравнения должны быть линейными в силу свойства однородности, которое мы приписываем пространству и времени. |
Тогда каждому моменту времени t покоящейся системы (K) соответствует определенное положение осей движущейся системы, и мы из соображений симметрия вправе допустить, что движение системы k может быть таким, что оси движущейся системы в момент времени t (через t всегда будет обозначаться время покоящейся системы) будут параллельны осям покоящейся системы. Представим себе теперь, что пространство размечено как в покоящейся системе K посредством покоящегося в ней масштаба, так и в движущейся системе k посредством движущегося с ней масштаба, и что, таким образом, получены координаты x, y, z и соответственно ξ, η, ζ. Пусть посредством покоящихся часов, находящихся в покоящейся системе, и с помощью световых сигналов указанным в §1 способом определяется время t покоящейся системы для всех тех точек последней, в которых находятся часы. Пусть далее таким же образом определяется время τ движущейся системы для всех точек этой системы, в которых находятся покоящиеся относительно последней часы, указанным в §1 способом световых сигналов между точками, в которых эти часы находятся. Каждому набору значений x, y, z, t, которые полностью определяют место и время событий в покоящейся системе, соответствует набор значений ξ, η, ζ, τ, устанавливающий это событие в системе k, и теперь необходимо найти систему уравнений, связывающих эти величины. Прежде всего ясно, что эти уравнения должны быть линейными в силу свойства однородности, которое мы приписываем пространству и времени. |
|
Если мы положим x' = x — vt то ясно, что точке, покоящейся в системе k, будет принадлежать определенный, независимый от времени набор значений x', y, z. Сначала мы определим τ как функцию от x', y, z, t. Для этой цели мы должны выразить с помощью некоторых соотношений, что τ по своему смыслу есть не что иное, как совокупность показаний покоящихся в системе k часов, которые в соответствии с изложенным в §1 правилом идут синхронно. Пусть из начала координат системы k в момент времени τ0 посылается луч света вдоль оси X в точку х' и отражается оттуда в момент времени τ1 назад, в начало координат, куда он приходит в момент времени τ2; тогда должно существовать соотношение
или, выписывая аргументы функции τ и применяя принцип постоянства скорости света в покоящейся системе, имеем
Если х' взять бесконечно малым, то отсюда следует: или
|
Если мы положим x' = x + vt то ясно, что точке, покоящейся в системе k, будет принадлежать определенный, независимый от времени набор значений x', y, z. Сначала мы определим τ как функцию от x', y, z, t. Для этой цели мы должны выразить с помощью некоторых соотношений, что τ по своему смыслу есть не что иное, как совокупность показаний покоящихся в системе k часов, которые в соответствии с изложенным в §1 правилом идут синхронно. Пусть из начала координат системы k в момент времени τ0 посылается луч света вдоль оси X в точку х' и отражается оттуда в момент времени τ1 назад, в начало координат, куда он приходит в момент времени τ2; тогда должно существовать соотношение
или, выписывая аргументы функции τ и применяя принцип постоянства скорости света в покоящейся системе, имеем Если х' взять бесконечно малым, то отсюда следует:
или
|
|
Необходимо заметить, что мы могли бы вместо начала координат выбрать всякую другую точку в качестве отправной точки луча света, и поэтому только что полученное уравнение справедливо для всех значений x', y, z, t. Если принять во внимание, что свет вдоль осей Y и Z при наблюдении из покоящейся системы всегда распространяется со скоростью,
то аналогичное рассуждение, примененное к этим осям, дает
Так как τ — линейная функция, то из этих уравнений следует
где a — неизвестная пока функция φ(v) и ради краткости принято, что в начале координат системы k при τ = 0 также и t = 0. |
Необходимо заметить, что мы могли бы вместо начала координат выбрать всякую другую точку в качестве отправной точки луча света, и поэтому только что полученное уравнение справедливо для всех значений x', y, z, t. Если принять во внимание, что свет вдоль осей Y и Z при наблюдении из покоящейся системы всегда распространяется со скоростью,
то аналогичное рассуждение, примененное к этим осям, дает
Так как τ — линейная функция, то из этих уравнений следует
где a — неизвестная пока функция φ(v) и ради краткости принято, что в начале координат системы k при τ = 0 также и t = 0. |
Вот откуда появилась эта функция a и почему она зависит от скорости пока не известно. Возможно для соблюдения размерности в формуле? Или по какой-то другой причине? Не знаю. И, соответственно, не известно, что будет в другом тексте.
|
Пользуясь этим результатом, легко найти величины ξ, η, ζ. С этой целью (как этого требует принцип постоянства скорости света в сочетании с принципом относительности) нужно с помощью уравнений выразить то обстоятельство, что свет при измерении в движущейся системе также распространяется со скоростью V. Для луча света, вышедшего в момент времени τ = 0 в направлении возрастающих ξ, имеем ξ = V τ или
Но относительно начала координат системы k луч света при измерении, произведенном в покоящейся системе, движется со скоростью V - v, вследствие чего Подставив это значение t в уравнение для ξ, получим
|
Пользуясь этим результатом, легко найти величины ξ, η, ζ. С этой целью (как этого требует принцип постоянства скорости света в сочетании с принципом относительности) нужно с помощью уравнений выразить то обстоятельство, что свет при измерении в движущейся системе также распространяется со скоростью V. Для луча света, вышедшего в момент времени τ = 0 в направлении возрастающих ξ, имеем ξ = V τ или
Но относительно начала координат системы k луч света при измерении, произведенном в покоящейся системе, движется со скоростью V + v, вследствие чего Подставив это значение t в уравнение для ξ, получим
|
Вот почему из формулы 1 получилась формула 2? Где потерялся еще один корень? Что? его впитала в себя функция φ(v)? Так на поверку она окажется единицей.
|
Если не делать никаких предположений о начальном положении движущейся системы и о нулевой точке переменной, то к правым частям этих уравнений необходимо приписать по одной аддитивной постоянной. |
Если не делать никаких предположений о начальном положении движущейся системы и о нулевой точке переменной, то к правым частям этих уравнений необходимо приписать по одной аддитивной постоянной. |
Дальше Эйнштейн доказывает, “что принцип постоянства скорости света совместим с принципом относительности”. И затем идет поиск значения функции φ(v) выясняется ее физический смысл. Оказалось, что функция φ(v)=1. И мне, к сожалению, не понятно какую физическую сущность представляет единица в данном случае. Координата – понятно, скорость или время то же понятны, а вот, физический смысл данной функции, кроме как данной пропорциональности между координатами, я не могу понять. Наверное, математические выкладки строги и точны. В результате преобразование приобрело вид:
|
|
|
В “§4. Физический смысл полученных уравнений для движущихся твердых тел и движущихся часов” Эйнштейн придает этим уравнениям физический смысл.
|
Рассмотрим твердый шар радиуса R, находящийся в покое относительно движущейся системы k, причем центр шара совпадает с началом координат системы k. Уравнение поверхности этого шара, движущегося относительно системы K со скоростью v, имеет вид ξ2 + η2 + ζ 2 = R2. Уравнение этой поверхности, выраженное через х, у, z, в момент времени t = 0 будет
|
Рассмотрим твердый шар радиуса R, находящийся в покое относительно движущейся системы k, причем центр шара совпадает с началом координат системы k. Уравнение поверхности этого шара, движущегося относительно системы K со скоростью v, имеет вид ξ2 + η2 + ζ 2 = R2. Уравнение этой поверхности, выраженное через х, у, z, в момент времени t ≠ 0 будет ?
|
|
Следовательно, твердое тело, которое в покоящемся состоянии имеет форму шара, в движущемся состоянии — при наблюдении из покоящейся системы — принимает форму эллипсоида вращения с полуосями.
В то время как размеры шара (а, следовательно, и всякого другого твердого тела любой формы) по осям Y и Z от движения не изменяются, размеры по оси X сокращаются в отношении
и тем сильнее, чем больше v. При v = V все движущиеся объекты, наблюдаемые из «покоящейся» системы, сплющиваются и превращаются в плоские фигуры. Для скоростей, превышающих скорость света, наши рассуждения теряют смысл; впрочем, из дальнейших рассуждений будет видно, что скорость света в нашей теории физически играет роль бесконечно большой скорости. |
В какой-то юмореске я видел и слышал такую сценку. Мать спрашивает сына ученика: “Ты, когда уберешься на своем столе?” Тот отвечает: “Сейчас”. Мать уточняет: “Сейчас – это когда?”. Будь жив Эйнштейн и я бы, имея такую возможность, задал ему такой вопрос: “t=0” – это когда? Вчера, сегодня, завтра, до большого взрыва или после взрыва? Или, когда это не было времени или его величина была равна 0? Естественно, что рассуждения о скорости вне времени не менее нелепы, чем судить, что будет с телами при скорости больше скорости света. В общем здесь большой знак вопроса. |
Как видите физический смысл уравнений в том, что они показывают, как в зависимости от скорости изменяется полуось эллипсоида или, более обще, размер тела вдоль оси X. Но, как говорил один герой из фильма “Иван Васильевич меняет профессию”: “Меня терзают смутные сомненья”. И терзают с двух сторон. Первое – математической. В параграфе 3 речь все время идет о четырехмерном пространстве. Обрабатываются все четыре координаты. А вот в параграфе 4 Эйнштейн придал координате времени нулевое значение (неважно, что нулевое, главное, что оно постоянное). Получился один эллипсоид при данной скорости. Так сказать, частный случай. Это примерно так, как если бы мы разговаривали в трехмерном пространстве о шаре, а потом начали любоваться его проекцией на плоскость. Ясно, как не катай шар по плоскости, его проекция на плоскости будет одна и та же. Но как только мы вспомним о третьей координате, так сразу же проекция изменит свой размер. Так может быть и с четырехмерным пространством произойдет то же самое?
Второе, есть еще такое размышление. Вот у нас есть шар. Начнем его ускорять, он будет сокращаться все больше и больше. Доведем его до какого-то размера, придав ему соответствующую скорость. Размер данной оси уменьшился. Если ничего дальше не делать, то эллипсоид будет двигаться с данной скоростью и данным размером. Но мы начнем его так же тормозить, то есть обратно ускорять, примерно так же, как ускоряли при увеличении скорости. Скорость будет падать и эллипсоид будет все больше полнеть и округляться. При нулевой скорости эллипсоид превратится в шар, на который все так же воздействует ускоряющая сила. Что должно происходить с шаром? Только что в эллипсоиде происходили под воздействием силы некие процессы, которые увеличивали ось эллипсоида. Сила осталась неизменной. Должны ли процессы, превращающие эллипсоид в шар, изменить свою ориентацию на сокращение оси? Разум, какой ни на есть, подсказывает, что в шаре процессы должны увеличивать ось. В самом деле, шар не мадам, которая, “ах, я пополнела, мне надо худеть”. К сожалению, многие ученые больше доверяют математической логике, нежели здравой. Математическая логика плохо объясняет физическую сущность явления.
И, наконец, что же в самом деле с телом при изменении его скорости? Рассмотрим такую простенькую геометрическую ситуацию. Вот перед вами три покоящиеся системы.
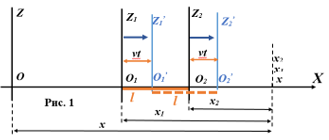
Как измеряются в них скорости? Измеряются расстояния x, x1 и x2, затем измеряется время появления луча света в точках О, О1, О2 и общей точке x, для этого Эйнштейн расставил везде синхронизированные часы. Деление полученных расстояний на время прохождения светом этих расстояний и дает искомую скорость в данной системе. Как оказывается если эти системы покоятся, то скорость света в каждой из них одинакова и равна приблизительно 300 000 км/сек. Это и постулировал Эйнштейн, чем сделал большое дело. Но что произойдет, если системы О1 и О2 придут в движение с одной и той же скоростью v вдоль оси X. Обе системы за одно и тоже время сдвинуться из точек О1 и О2 на одно и то же расстояние vt в положение О1’ и О2’. Думаю, математика этого отрицать не будет. И если бы между точками О1 и О2 находился стержень длины l, то он такой же длины должен быть между точками О1’ и О2’. Но математика Эйнштейна показывает, что стержень длины l сократится на величину
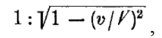
Почему же так? Давайте рассмотрим рисунок 2.
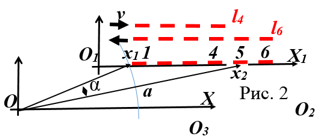
Вынесем покоящегося наблюдателя в сторону от оси X1 в точку О. Пусть сначала обе системе покоятся. В системе О1 на оси расположен стержень длиной в 6 условных единиц. На единицах 1 и 5 расположены отражающие элементы, мы должны видеть, то что измеряем. Неподвижный наблюдатель посылает в точки x1 и x2 лучи и видит элементы 1 и 5 и решает, что длина стержня равна 5 единицам. С какой бы точки он не измерял этот стержень, он получит результат 5. Обе системы покоятся. Теперь пусть система О1 начнет удаляться от покоящейся системы со скоростью v. Наблюдатель из точки О запускает в том же направлении лучи с таким же углом α, как и в случае измерения неподвижного стержня. Линейка или шаблон должен быть одним тем же, не зависимо от того движется какая-то система или нет. В противном случае мы будем измерять перспективу: сходящиеся рельсы или удаляющиеся, или приближающиеся объекты. Как только лучи запущены один из них долетает до точки x1 и снимает информацию 1, второй луч в это же время находится в точке а. Ему для съема информации надо пролететь еще путь равный а-x2. И пока он преодолевает этот путь, стержень, двигаясь со скоростью v, может в точку x2 поставить элемент 4, и наблюдатель может заключить, что он видит стержень длиной l4, а не l5, как в случае покоящегося стержня. Если стержень будет двигаться в обратном направлении (системы будут сближаться), в точке x2 окажется элемент 6, и наблюдателю покажется, что пролетает стержень длиной l6. Если покоящаяся система будет расположена в точке О2, то наблюдатель в этой системе будет видеть все наоборот в отличие от того, что видит наблюдатель в точке О. Наблюдатель в системе О3 скажет: “Вы оба дураки, стержень свою длину не меняет вовсе”.
Из всех этих довольно простых рассуждений можно сказать, если только исходитьиз математических выкладок Эйнштейна, что длина стержня или оси эллипсоида не должна зависеть от их скоростей. Но на самом деле любое тело излучает, ибо оно состоит из частиц, которые при их ускорении излучают или поглощают фотоны различных энергий. Излучить они могут только часть себя. В результате частицы просто физически уменьшаются в объеме, переходят на другие уровни, чем изменяют размеры атомов, молекул и, в результате, всего тела.
Вывод такой: при изменении скорости тело изменяется в объеме, а не только по одной из осей. Физически возможности выкладок данной части СТО можно применить только к методике измерений, но не к физическим свойствам тел.
