Чуть раньше мы рассматривали центробежную силу и выяснили, что ее источником является инерция, а сама инерция представляется излучаемыми фотонами. Оказывается, что и гироскопические силы тесно связаны с фотонами.

Силу инерции мы обнаружили давно – стоит потянуть любое тело динамометром, и мы всегда увидим, что тело сопротивляется с какой-то силой. Эту силу легко рассчитать или измерить. Она хорошо описана законами Ньютона. Но физический носитель этой силы без погружения в квантовый мир увидеть не возможно. Можно отвергать или оспаривать предложенную модель инерции и, следовательно, центробежной силы, но автор уверен, что без привлечения квантового мировоззрения понять данные явления не удастся.

Такая же ситуация наблюдается и с гироскопическими силами. Кажется, мы все о них знаем, рассчитываем их и пользуемся результатами расчетов в практике. Но вот появляется гайка Джанибекова, и требуются значительные усилия научного сообщества, чтобы осмыслить данное явление. Конечно, могло случиться так, что Джанибеков мог бы и не обнаружить данное явление, и мы бы спокойно жили и не думали о перевороте Земли.  Правда, даже если мы будем все знать о перевороте Земли, мы ничего поделать с этим явлениям не сможем, но как-то подготовится к этому катаклизму, было бы желательно. 

Рассмотрим поведение волчка в различных состояниях.

1. Не вращающийся волчок в невесомости будет сохранять свое положение сколь угодно долго. На Земле положение волчка стоящего на оси вращения неустойчиво. Малейшее смещение оси вращения Оа волчка от вертикальной оси Оо приводит к тому, что часть 2 (относительно вертикальной плоскости) волчка становится тяжелее части 1 и волчок падает. Какие физические процессы происходят в этом случае в волчке

Гравитационное воздействие F₂ на часть 2 больше гравитационного воздействия F₁ на часть 1 и волчок падает в сторону большей силы.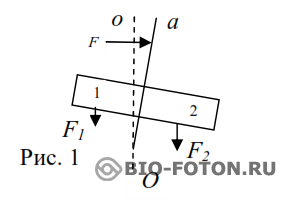

1. Приведем волчок во вращение вокруг оси Оо. При определенной скорости вращения волчок перестает падать и приобретает устойчивое состояние, из которого невозможно его вывести даже при отклонении оси волчка Оа от оси вращения.

Спрашивается: почему он не падает? Классический ответ: он не падает, потому что сохраняется момент вращения. А почему и какими силами сохраняется момент вращения? Почему, например, при 10 оборотах в минуту этот момент вращения не сохраняется и волчок падает, а при 1000 оборотов в минуту этот же самый волчок сохраняет момент вращения так, что его трудно свалить?  Ведь когда сила F отклонит ось волчка от оси вращения, то сила F₂ будет больше силы F₁.Что скомпенсирует силу F₂ – F₁? Это же физическая величина, это гравитация. Мы прыгаем, запускаем ракеты и тому подобное, чем компенсируем воздействие силы гравитации и в этих случаях мы знаем, чем их компенсируем. А в случае вращения, чем компенсируем силу гравитации? Есть что-нибудь физическое, что уравновешивает эту силу или, может быть, эта сила исчезает? А если эта сила исчезает, то почему в невесомости волчок сохраняет свое положение и при действии силы на ось вращения он не наклоняется, а смещается параллельно? Происходят ли какие-нибудь изменения во вращающемся теле по сравнению с неподвижным телом?

Рассмотрим такую модель Рис. 2.

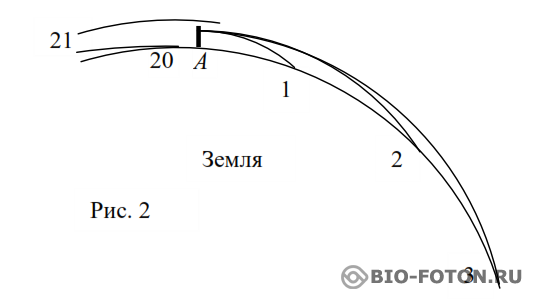
Выровняем Землю до идеального шара, уберем изостазию и атмосферу. Поставим в точке А башню, на башне поставим орудие и начнем стрелять из него параллельно Земле. Первый снаряд пусть ляжет в точке 1. Увеличим скорость снаряда, он пролетит до точки 2. Будем и дальше увеличивать начальную скорость снаряда. Он будет ложиться все дальше и дальше: 3, 4 …20, 21. 21-й снаряд тоже может лечь где-нибудь в точке (1, 2, 3 и т.д.), но при определенной скорости, для Земли это примерно 8 км/сек, он будет кружиться вокруг Земли по окружности. Если скорость будет больше указанной скорости, то снаряд будет двигаться по эллиптической траектории. А при скорости примерно 11 км/сек покинет Землю.

Если бы мы стреляли снарядами с пружинными весами, на которых лежит килограммовая гиря, то мы наблюдали бы такое явление.  В первом снаряде после выстрела, весы показали бы сначала вес гири чуть меньше килограмма, но в конце полета гиря потяжелела бы до своего номинала. Во втором снаряде весы показали бы еще меньший начальный вес гири, в третьем еще меньше и так далее. И когда снаряд достигнет космической скорости, весы будут показывать нулевой вес, и он не будет увеличиваться. Значит, и сам снаряд при такой скорости будет иметь нулевой вес, т.е. ничего не будет весить. Такое явление будет наблюдаться при любом горизонтальном направлении полета снаряда.

А теперь на этой башне расположим горизонтально диск и начнем его раскручивать. Выделим мысленно какой-нибудь кусочек диска. При некоторой скорости вращения он станет легче как снаряд, упавший в точку 1. При увеличении скорости вращения, он станет легче как снаряд, упавший в точку 2 и так далее. При космической скорости он будет невесом. И так со всеми частями диска. Самые тяжелые, равными примерно собственному весу, будут кусочки, расположенные на оси вращения. А дальше от оси вращения кусочки будут все легче и легче. Хотя, заметьте, согласно теории относительности эти кусочки с возрастанием скорости должны приобретать все большую и большую массу.  Правда, это утяжеление должно быть незначительным, так эта скорость далека от световой. Да и возрастание массы происходит не абсолютно а относительно. Если взять диск с длиной окружности равной 1 метр, то при 8 000 оборотов в секунду, кусочек окружности будет двигаться с космической скоростью и его вес будет нулевым. Весь вращающийся диск будет легче неподвижного. И чем больше будет скорость вращения, тем легче будет диск. Если бы это был обруч, то его можно было бы раскрутить до невесомости. Жаль только, нет такого материала, крепость которого позволила бы так раскрутить обруч.

Но почему же обруч стал невесом? На этот вопрос просто ответить, если принять модель гравитации, предполагающую, что гравитация это резонансное поглощение фотонов. В статье “О кванте подробно” мы предположили, что квантов, а, соответственно и фотонов, может быть 8 видов и какие из них участвуют в гравитационном взаимодействии, мы не знаем. Вероятнее всего, что любые.

Мы знаем, что электроны при ускорении излучают фотоны и знаем, что чем больше скорость электрона, тем большей энергии они излучают фотоны. При увеличении скорости электрона из него, если можно так сказать, “вымываются” фотоны малых энергий и остаются фотоны с большими энергиями.  Это значит, что электроны теряют свои резонансные свойства по отношению к фотонам определенной энергии и приобретают свойства для взаимодействия с фотонами большей энергии. Это значит, что в атомах произошли физические изменения, причиной которых является изменение их скорости под воздействием внешних сил. Электроны излучили определенные фотоны, их заряд и масса изменились, они ближе “прижались” к ядру, объем диска или обруча уменьшился. 

Мы живем в среде фотонов с энергией соответствующей горбу кривой излучения абсолютно черного тела (Рис. 3).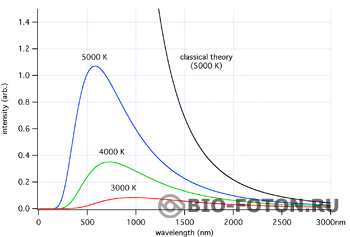

Это значит, что мы живем при излучениях с длиной волны, примерно, от 400 нм до 1500 нм. Эти фотоны поставляются нам Солнцем и Землей. В Земле бурлят какие-то процессы: передвигаются земные плиты, кипит магма, движутся массы воды и атмосферы, идут химические реакции, в том числе и в живой материи, и тому подобное. Но во всех этих явлениях работают фотоны с указанной выше энергией. Если нам нужны фотоны других энергий то мы либо расщепляем ядро, либо строим рентгеновскую трубку, либо строим микроволновку, либо строим радиопередатчики и т.д. В общем, все, что за пределами этого горба, мы, в основном, получаем искусственно. В природе, в частности на Земле такого излучения мало.

И вот когда мы раскручиваем обруч, мы выводим резонансные свойства электронов с области излучений горба на крылья горба, где излучение слабое или вообще нет излучателей фотонов данной энергии. А раз нет резонансных пар, значит, нет и проявлений гравитации. И наш обруч ничего не весит. Может быть, так, что на Земле, при данных оборотах, он ничего не весит, а на другой планете при этих оборотах он будет иметь определенный вес. Можно уверенно сказать, что на Солнце обруч следует раскрутить до большей скорости, чтобы он стал невесомым. На Солнце большие массы субстрата передвигаются с большими скоростями, нежели на Земле, чем генерируют значительно больший спектр фотонов.

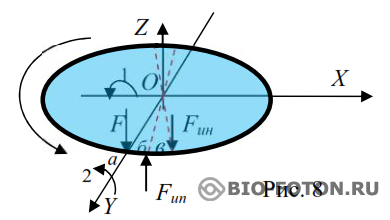
Но все же: почему не падает волчок? Посмотрим на Рис. 4.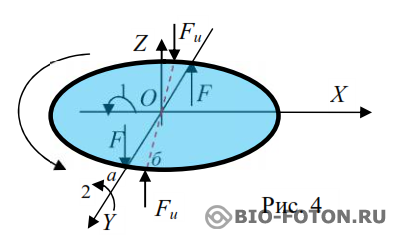

Диск вращается вокруг оси Z. Подействуем на точку а диска силой F, которая придаст данной точке некоторое ускорение. Пусть импульс Ft будет коротким по отношению к скорости вращения диска, то есть за время действия данного импульса диск проворачивается на незначительный угол. Эта сила будет стремиться повернуть диск вокруг оси X, стрелка 1. Электрон точки а, получив ускорение, обязан излучить инерционный фотон. А мы знаем, что для излучения фотона требуется определенное время. Чем большей энергии излучается фотон, тем дольше он излучается. Пока фотон излучается, ничего не происходит. Все замирает или движется по инерции. В нашем случае, пока инерционный фотон находится в процессе генерации, диск вращается вокруг оси Z и вокруг оси X, со скоростью приданной импульсом силы F. За время генерации фотона точка а диска сместится в положение б, где и будет излучен инерционный фотон F_и. И как видим из рисунка, этот импульс будет не только противиться силе F, пытающейся опрокинуть диск вокруг оси X, но и сам будет стремиться повернуть диск вокруг оси Y по стрелке 2.

Чем больше сила F, тем большее ускорение точки а, тем более мощный генерируется фотон и тем дольше он генерируется. В результате большего времени генерации возрастает плечо момента аб. Обратная связь оказывается отрицательной и поэтому система обладает устойчивостью. Естественно, что чем больше скорость вращения, тем более устойчивая система.

Можно сделать вывод, что волчок не падает из-за наличия инерционных фотонов.

Еще раз напомним, что это не какие-то особые фотоны, а те которые мы наблюдаем в виде всевозможных излучений, в том числе и в виде торсионных полей. Очевидно, что все эти виды излучений обладают спектром, сильно совпадающим со спектром абсолютно черного тела.

Вращающийся диск это простейший гироскоп. Соотношение инерционной силы, возмущающей силы и способа приложения этой силы может приводить к разнообразным видам поведения гироскопа.

Если раскрутить волчок с острой опорой и поставить его на плоский стол под углом, то наклоненный волчок не упадет на стол, а начнет вращаться вокруг вертикальной оси с некоторой угловой скоростью (Рис. 5).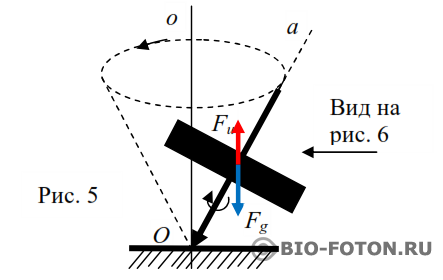

Сила веса F_g, как и в случае силы F (Рис. 4), будет стремиться опрокинуть волчок. В какой-то момент она придаст ускорения электронам волчка и заставит их излучить инерционные фотоны, которые в сумме создадут силу инерции F_и, которая всегда окажется больше силы F_g, если волчок не упал. Дальше мы увидим, что будет, если эти две силы будут сравниваться. Но эти силы инерции из-за задержки генерации фотонов выходят из плоскости рисунка и пытаются развернуть волчок в плоскости перпендикулярной плоскости рисунка. Но точка опоры волчка неподвижна и ось волчка поворачивается относительно точки опоры по стрелке 2 (Рис. 6).

Ось волчка начинает двигаться, описывая боковую линию конуса. Такое движение гироскопа называется прецессией. Расчеты, которые можно найти в любом учебнике, показывают, что скорость прецессии в первом приближении описываются формулой: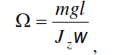

где Ω – угловая скорость прецессии, w– скорость вращения гироскопа,  Ɩ – расстояние от центра тяжести гироскопа до точки опоры,  J_z – момент инерции. 

Как видим, из формулы следует, что, чем выше скорость вращения гироскопа, тем меньше скорость прецессии. А согласно нашим рассуждениям (рисунок 6) следует, что чем выше скорость вращения, то генерируется более мощный инерционный фотон. Следовательно, появлялся больший момент для вращения гироскопа относительно оси Y, что должно приводить к увеличению скорости прецессии.

Действительно, при окружной скорости диска v_1д и скорости наклона гироскопа v_г, диск наклоняется к нам, результирующая скорость будет равна V₁, которая генерирует фотон силы F_1и. Эта сила будет стремиться повернуть волчок по стрелке 2 вокруг оси Y. Эта сила представляет силу прецессии. Если окружная скорость диска будет больше, например, v_2д, то соответственно должен быть генерирован инерционный фотон большей мощности, который создаст большую силу прецессии F_1и. Это будет справедливо, если скорость v_г будет одна и та же.

Формула и опыт показывает, что скорость падает. Но никакого противоречия здесь нет. Выше мы видели, что при увеличении скорости вращения гироскопа он становится легче, т.е. уменьшается величина mg. Это значит, что хотя инерционные импульсы и становятся больше, зато еще больше сокращается их количество. Поэтому и получается такой результат. В общем, это все надо считать, а я не умею это делать.           

Мы видели, что равновесное положение гироскопа является динамическим. Как только какая-нибудь сила пытается вывести его из равновесного состояния, он излучает инерционные фотоны, которые возвращают его в прежнее состояние. Силы гравитации непрерывно пытаются нарушить равновесное состояние, поэтому ось гироскопа все время “дрожит”. Это практически не заметное “дрожание” в установившемся режиме. При запуске гироскопа или при некоторых возмущениях “дрожание” становится заметным и называется оно нутацией. 

Чем резче мы поставим на опору под углом раскрученный гироскоп, тем на большую величину опустится центр тяжести гироскопа от плоскости равновесия (ось гироскопа будет расположена на линии Оа1), в которой будет двигаться центр тяжести при равновесном состоянии (ось будет расположена по линии Оа) (Рис. 7).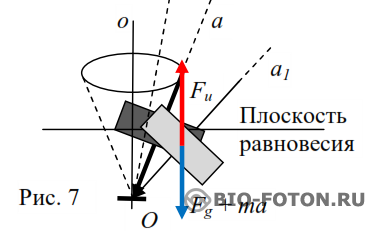

Импульс силы F_g + ma спровоцирует генерацию инерционного фотона силы F_и, которая поднимет центр тяжести гироскопа. А поскольку эта сила инерции больше силы требующейся для равновесного состояния, то ось гироскопа окажется на линии Оа₂. Затем ось гироскопа снова двинется в направлении линии Оа₁. Силы трения в опоре и сопротивления воздуха будут уменьшать составляющую ma, что приведет к затиханию колебаний, вызванных резкой постановкой гироскопа, но  “дрожание” оси гироскопа из-за нутаций останется.

В статье Интернет “ Лекция 11. Гироскопы” (Башкирский государственный аграрный университет) есть такие картинки (Рис. 96) с описанием.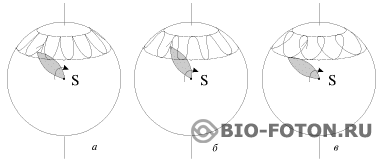

“Характер траектории, по которой движется вершина гироскопа, зависит от начальных условий. В случае рис. 96,а гироскоп был раскручен вокруг оси симметрии, установлен на подставке под некоторым углом к вертикали и осторожно отпущен. В случае рис. 96,б ему, кроме того, был сообщен некоторый толчок вперед, а в случае рис. 96,в - толчок назад по ходу прецессии”.

Как видим, есть некоторая сила, которая заставляет двигаться ось гироскопа по таким замысловатым линиям. Эта сила не является силой трения, ибо дальше говорится:   

“Если за счет трения в опоре нутации гасятся быстрее, чем вращение гироскопа вокруг оси симметрии (как правило, так и бывает), то вскоре после "запуска" гироскопа нутации исчезают и остается чистая прецессия”.               

Стало быть, если бы не было сил трения, то нутации не исчезали бы. Какие-то силы  добавлялись бы в движение гироскопа, и он бы двигался таким образом. Что это за силы и как они действуют? Рис. 8.